Nonlinear Equations; Find sol(비선형 방정식 해 찾기)
- The Relaxation Method
- Binary Search-Bisection Method
- Newton’s Method
- Secant Method[Boundary condition 주어진 방정식 해를 찾을 때 사용]
- The Relaxation Mehod(RM)
x=f(x); single variable equation
1. guess the initial value of x0
2. plug it into f(x) and set x1=f(x0)
3. set x0=x1 and repeat the procedures (1) and (2) until x1 converges to a certain value
초기값에 의존해서 하나의 해만 찾아냄
# x=2-exp(-x)
from math import exp
def f(x):
y=2-exp(-x)
return y
x=1.0
for i in range(10):
x=f(x) # same as tmp=f(x); x=tmp
#print(f(x)-x)
print(x)
1.6321205588285577
1.8044854658474119
1.8354408939220457
1.8404568553435368
1.841255113911434
1.8413817828128696
1.8414018735357267
1.8414050598547234
1.8414055651879888
1.8414056453310121
However, there are some solutions to some equations that you cannot
find by this mehod no matter what starting value you choose
import numpy as np
# x=exp(1-x^2)
def f(x):
y=np.exp(1-x**2)
return y
x=0.0
for i in range(10):
x=f(x) # same as tmp=f(x); x=tmp
#print(f(x)-x)
print(x)
2.718281828459045
0.0016798410570681988
2.71827415784286
0.001679911110814363
2.718274157203078
0.00167991111665744
2.7182741572030253
0.0016799111166579221
2.7182741572030253
0.0016799111166579221
x= 1−lnx 로 바꾸지 않으면, 해에 수렴하지 못함 (실제 해는 1)
|f′(x∗)| < 1 인 경우에만 해를 찾을 수 있음
해에서 기울기가 1이상인 경우, inverse function은 해에서 기울기 크기가 1보다 작기 때문에 사용 가능
(x와 만나는 해는 f(x)와 f(x)의 역함수가 동일하기 때문에 사용해도 무방); x= 1−ln
error:
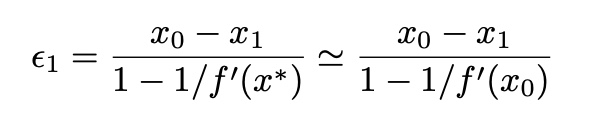
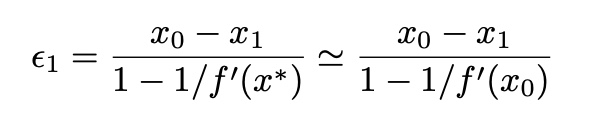
- Binary Search-Bisection Method
f(x)=0
solution range을 사전에 알면 값을 구할 수 있음
The simplest and the most intuitive method
Assume that we know the root x is the interval [a, b]
1. set x0=(a+b)/2
2. if f(a)f(x0)<0 then let b=x0
3. else set a=x0
4. repeat 1-3 untile abs(a-b)<=delta(tolerance)
5. if( abs(a-b) )<=delta then set x=(a+b)/2
import math
def f(x):
return math.exp(1-x**2)-x
a=0.0
b=2.0
delta=1.0e-6
err=1.
while(err>delta):
x0=(a+b)/2
if f(a)*f(x0)<=0:
b=x0
else:
a=x0
err=np.abs(a-b)
x_star=(a+b)/2
print(x_star)
- Newton-Raphson Method(NRM)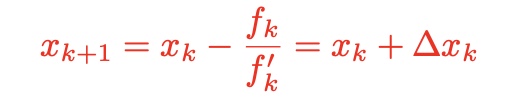
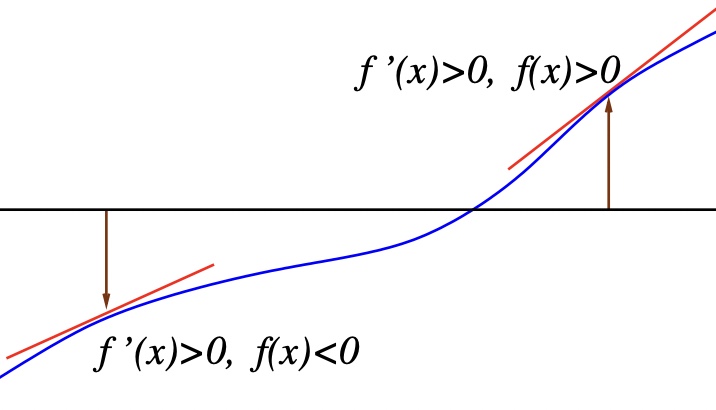
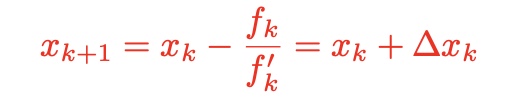

import numpy as np
import math as m
def f(x):
return x-m.exp(1-x**2)
def df(x):
return 1+2*x*m.exp(1-x**2)
x=1.5
tolerance=1e-6
delta=1.0
for i in range(10):
delta=-f(x)/df(x)
x+=delta
while abs(delta)>tolerance:
delta=-f(x)/df(x)
x+=delta
hypobolic tangent
import math as m
import numpy as np
import matplotlib.pyplot as plt
def f(x, u):
return m.tanh(x)-u
def df(x):
return 1/m.cosh(x)**2
ulist=np.linspace(-0.99, 0.99, 100)
px=[]
x=0
for u in ulist:
tolerance=1e-5
delta=1.0
while abs(delta)>tolerance:
delta=-f(x, u)/df(x)
x+=delta
px.append(x)
plt.plot(ulist, px, "ro")
plt.show()
- Secant Method(SM)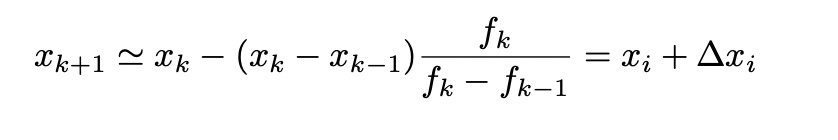
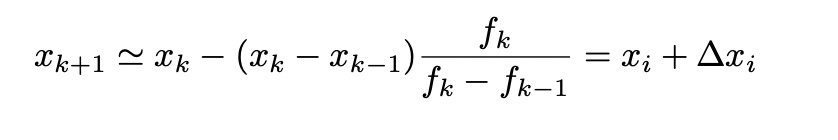
generalized version of Newton-Raphson method
import math as m
import numpy as np
def f(x):
return x-m.exp(1-x**2)
def df(x, dx):
return (f(x)-f(x-dx))/dx
x=1.5
tolerance=1e-6
delta=1.0
dx=0.1
while abs(delta)>tolerance:
delta=-f(x)/df(x, dx)
x+=delta
dx=delta